分类算法之逻辑回归（Logistic Regression）

  一、逻辑回归简介    

将输入特征与某个类别之间的概率关系建模，特别用于解决二分类问题，通过给定的n组数据（训练集）来训练模型，并在训练结束后对给定的一组或多组数据进行分类，其中的每一组数据都是由p个指标构成--主要用于二分类问题

二、逻辑回归的理论推导

 1、sigmoid函数，也称为逻辑函数

                                                      

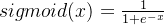
      sigmoid 函数将输入变换成（0，1）上的输出,找一个关于x的函数来得出分类结果

      

2、 初步思路：

一个二分类问题给的条件：

分类标签Y {0，1}，特征自变量X{x1，x2，……，xn}

如何根据我们手头上的特征来判断它应该属于哪个类别

由一个线性模型来由x预测y 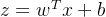    但这样的函数图像类似一条斜线，难以到达想要的（0或1）的取值，引入sigmoid函数（二者结合的目的是要将线性模型的输出映射到（0，1）区间内

3、将线性模型与sigmoid函数合体

将线性模型与sigmoid函数合体 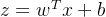   （z可以是任何实数）

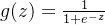    将线性模型的输出z映射到（0，1）之间，该函数的特点是，当z趋于正无穷时，g(z) 趋于1 ，当z趋于负无穷，g(z)趋于0，使得线性模型的输出结果变为一个概率值

4、条件概率

   两边同时取对数可得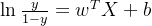

将y视为样本x作为正例的概率，那么1-y则为样本x作为反例的概率，二者的比值为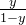

所以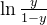被称为对数几率

因此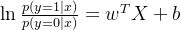

所以推出了：

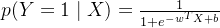
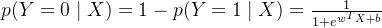
5、极大拟然估计

思想：如果一个事件发生了，那么发生这个事件的概率就是最大的。对于样本i，其类别为。对于样本i，可以把h(Xi)看成是一种概率。yi对应是1时，概率是h(Xi)（即Xi属于1的概率，即上面的p(Y=1|X)）；yi对应是0时，概率是1-h(Xi)（Xi属于0的概率，即上面的p(Y=0|X)）。

即有：

该式子表示生成观测到所有训练数据样本（即类别标签）的概率，我们想找到一组参数，在这组参数下，模型生成观测数据的概率最大（一组最优参数能够很好的拟合训练数据）

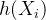 给定输入特征Xi 和模型参数，该函数输出样本属于正类的概率

yi表示第i个样本的真实标签，，它的值要么时0要么是1（主要为处理二分类问题）

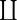表示连乘

h(xi)表示第i个样本属于正类的概率 1-h(xi)表示第i个样本属于负类的概率

如果样本 i 的真实标签是 y_i=1（正类），那么它的正确分类概率应该是 h(X_i)。相反，如果样本 i 的真实标签是y_i=0（负类），那么正确分类的概率应该是 1-h(X_i)。我们需要一种通用的表示方法，既可以表示正类的概率，也可以表示负类的概率。

用指数形式来表示正确分类的概率，我们将两种情况合并为一个统一的表达式，无论y_i的值是多少，都可以正确的给出样本i的正确分布概率

我们需要计算所有训练样本的联合概率，样本是独立同分布的，确保整个数据集的联合概率被计算在内，之后，我们可以通过最大化这个拟然函数来估计模型参数

对它取对数（将连乘变成累加），并除以样本总数n（我们关心的是平均损失，归一化损失，使其不受样本总数的影响，减少梯度爆炸出现的概率），再乘以负一（将求最大值问题转成求最小值问题）

化简完得到

  未知数为w和b，我们的目标是找到使J（w）最小化的w和b，我们将使用训练数据（特征和标签）以及优化算法（梯度下降）来迭代更新w和b

J（w)输出的结果是模型预测输出与真实标签之间的偏差（误差）

6、梯度下降求最小值w

通过J(w)对w的一阶导数来找下降方向，并以迭代的方式来更新参数

 这里的k代表的是第k次迭代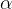；是我们设定的学习率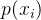；就是我们上面所说的 ）

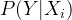三、多类逻辑回归

假设一共分为K类，那么公式换为以下两个：

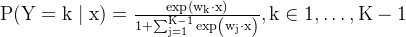
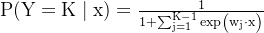
四、正则化

 过拟合：是指在训练机器学习模型时，模型在训练阶段过渡拟合了训练数据，以至于它不能很好的适应新数据

我们采取正则化，来避免过拟合，正则化可以避免过拟合的原因就是它降低了特征的权重，使得模型更简单。

主要思想：保留所有的特征变量，因为我们不太清楚要舍掉哪个特征变量，并且又想尽可能保留信息。所以我们只能是惩罚所有变量，让每个特征变量对结果的影响值变小，这样的话你拟合出来的模型才会更光滑更简单，从而减少过拟合的可能性。

1、L1正则化 是指在损失函数上添加一个正则化项，起到约束模型参数的作用，这个正则化项是权重向量中每个元素的绝对值之和

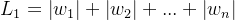（不是很理解？）

损失函数=原始损失函数+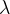*L1

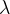是正则化系数，用于控制对权重的惩罚力度，如果λ设置的太高，会导致模型欠拟合，如果λ的值设置的太低，将无法有效解决过拟合问题

作用：L1正则化有特征筛选的作用，对所有参数的惩罚力度都一样，可以让一部分权重变为零（降维），因此产生稀疏模型，能够去除某些特征（权重为0则等效于去除）

2、L2正则化

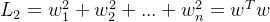
作用：使各个维度权重普遍变小，减少了权重的固定比例，使权重平滑

五、逻辑回归的优缺点

优点：

1、简单易实现：逻辑回归模型的原理简单，易于实现

2、计算复杂度低：参数数量较少，仅有权重和偏置。

3、输出具有概率意义：逻辑回归模型的输出结果可解释为属于某一类的概率，方便进行类别概率分析和阈值调整。这可以帮助我们根据不同业务需求来调整分类决策的阈值。

4、可扩展性强：逻辑回归与其他技术（如L1/L2正则化、梯度下降等）可以很好地集成，从而实现更多功能（如特征选择、避免过拟合等）。

缺点：

1、表达能力有限：逻辑回归模型是一个线性分类器，对于非线性可分问题的表达能力有限。当底层数据模式复杂时，逻辑回归的性能可能受到影响。

2、对异常数据敏感：训练数据中的噪声和异常点可能对模型的参数估计产生较大影响，从而导致模型泛化能力减弱。

3、难以处理多重共线性：逻辑回归在处理特征之间具有多重共线性的问题时，会遇到困难。当特征之间高度相关时，模型参数的估计可能不稳定，尤其是在使用最大似然估计方法时。