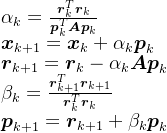本文旨在总结线性方程组求解的相关算法,特别是Krylov子空间法的原理及流程。
注1:限于研究水平,分析难免不当,欢迎批评指正。
注2:文章内容会不定期更新。
零、预修
0.1 共轭转置
对于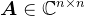 、
、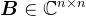 ,若矩阵
,若矩阵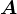 第
第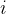 行第
行第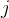 列元素
列元素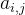 的共轭等于矩阵
的共轭等于矩阵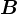 第
第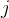 行第
行第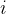 列元素
列元素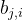 ,即
,即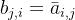 ,则称矩阵
,则称矩阵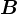 是矩阵
是矩阵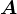 的共轭转置矩阵,记作
的共轭转置矩阵,记作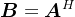 。
。
可以看出,若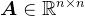 ,则
,则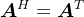 。
。
0.2 Hermite矩阵
对于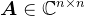 ,若
,若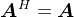 ,则称矩阵
,则称矩阵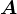 为Hermite矩阵。
为Hermite矩阵。
可以看出,若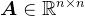 ,则
,则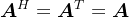 ,即实数域的Hermite矩阵即是对称矩阵。
,即实数域的Hermite矩阵即是对称矩阵。
0.3 Hessenberg矩阵
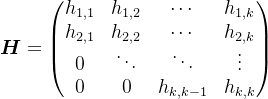
0.4 Cholesky分解
对于正定矩阵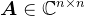 ,则有
,则有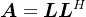 ,其中,矩阵
,其中,矩阵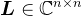 是下三角矩阵,矩阵
是下三角矩阵,矩阵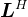 是矩阵
是矩阵 的共轭转置。
的共轭转置。
若对称正定矩阵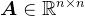 ,则有
,则有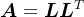 ,其中,矩阵
,其中,矩阵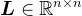 是下三角矩阵,矩阵
是下三角矩阵,矩阵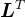 是矩阵
是矩阵 的转置。
的转置。
0.5 Arnoldi分解
设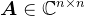 ,则有
,则有 ,其中
,其中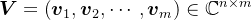 ,
,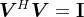 ,
,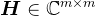 ,
,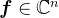 ,
, ,
,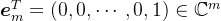 。
。
下面如无特殊说明,均仅讨论实数域内的线性方程组。
一、直接法求解线性方程组
1.1 LU分解
设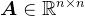 ,若对于
,若对于![数值线性代数: Krylov子空间法 k\in \left [ 1,n \right ]](https://js.wyfx2014.com/zb_users/upload/2024/03/20240316075803171054708350232.png) ,均有
,均有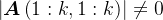 ,则存在唯一的单位下三角矩阵
,则存在唯一的单位下三角矩阵 和上三角矩阵
和上三角矩阵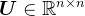 ,使得
,使得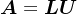 ,并且
,并且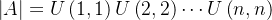 。
。
1.2 Cholesky分解
若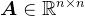 对称正定,则有
对称正定,则有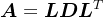 ,其中,
,其中, 为单位下三角矩阵,
为单位下三角矩阵,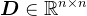 为对角元均为正数的对角矩阵。
为对角元均为正数的对角矩阵。
二、 总论:迭代法求解线性方程组的一般思路
对于非奇异矩阵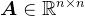 ,
,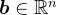 ,使用迭代法求解线性方程组
,使用迭代法求解线性方程组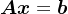 过程中,一般需要以下流程进行:
过程中,一般需要以下流程进行:
- 给定一个初始向量
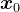 ;
; - 构造一个递推公式
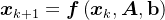 ;
; - 不断递推
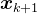 ,使其近似收敛于
,使其近似收敛于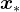 ;
;
下表列出了若干迭代算法的迭代公式。
| 方法 | 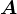 | 迭代公式 | 备注 |
| Jacobi迭代 | 非奇异 | 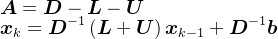 | |
| Gausss-Seidel迭代 | 非奇异 | 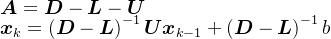 | |
| SOR迭代 | 非奇异 | 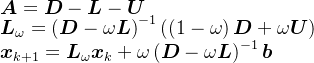 | |
| Steepest Descent | 对称正定 | 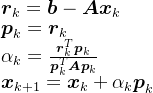 | |
| Conjugate Gradient | 对称正定 | 当 当1" src="https://latex.csdn.net/eq?k%3E1" />时 |
三、Projection Methods
投影法在较小的线性空间内寻找满足精度要求的近似解,也即在某个线性空间内寻找真解的投影。这其实就是投影法得名的原因。
对于非奇异矩阵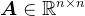 ,考虑线性方程组
,考虑线性方程组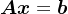 ,其中,
,其中, ,
,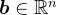 。
。
令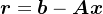 ,首先,构造列满秩矩阵
,首先,构造列满秩矩阵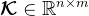 与
与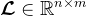 ,其中
,其中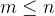 ;然后,设真解
;然后,设真解 在线性空间内
在线性空间内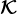 的投影为
的投影为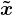 ,即
,即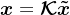 ,令其满足Petrov-Galerkin条件,即
,令其满足Petrov-Galerkin条件,即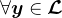 ,均有
,均有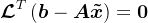 。
。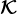 称为搜索空间,
称为搜索空间,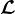 称为约束空间。若
称为约束空间。若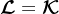 时,称为正投影算法,否则称为斜投影算法。
时,称为正投影算法,否则称为斜投影算法。
若令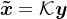 ,则有
,则有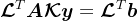 ,其中
,其中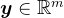 ,
,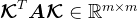 ,
,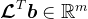 。可以看出,投影法实际上是将
。可以看出,投影法实际上是将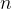 阶线性方程组转化为了
阶线性方程组转化为了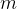 阶线性方程组(
阶线性方程组(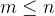 )。
)。
讨论:
- 若
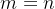
以正则化方法为例,即
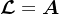 ,
,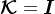 ,由于
,由于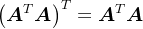 ,另外,
,另外,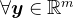 ,0" src="https://latex.csdn.net/eq?%5Cboldsymbol%7By%7D%5E%7By%7D%5Cboldsymbol%7BA%7D%5E%7BT%7D%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%3D%5Cleft%20%28%20%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%5Cright%20%29%5E%7BT%7D%5Cleft%20%28%20%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%5Cright%20%29%3E0" />,即
,0" src="https://latex.csdn.net/eq?%5Cboldsymbol%7By%7D%5E%7By%7D%5Cboldsymbol%7BA%7D%5E%7BT%7D%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%3D%5Cleft%20%28%20%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%5Cright%20%29%5E%7BT%7D%5Cleft%20%28%20%5Cboldsymbol%7BA%7D%5Cboldsymbol%7By%7D%5Cright%20%29%3E0" />,即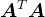 是对称正定矩阵。因此,正则化方法实际上将一般矩阵线性方程组
是对称正定矩阵。因此,正则化方法实际上将一般矩阵线性方程组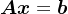 转化为对称正定线性方程组
转化为对称正定线性方程组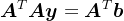 。
。- 若
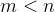
由于
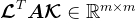 ,
,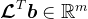 ,线性方程组的规模由
,线性方程组的规模由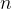 阶降为了
阶降为了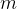 阶。因此,可以通过投影法可将问题转换为更为简单的子问题,然后再进行求解。
阶。因此,可以通过投影法可将问题转换为更为简单的子问题,然后再进行求解。以求解非对称线性方程组的Arnoldi方法为例,即
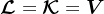 ,其中,
,其中, ,
,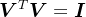 ,
,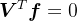 。则
。则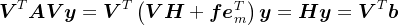 。
。综合上述讨论,可归出结投影法的操作流程:
- 使用投影法将问题转化为较易求解的子问题;
- 使用合适的方法求解子问题。
四、Krylov Subspace Methods
Krylov子空间法本质上也是一种投影法,其核心思想是在较小维度的Krylov子空间内寻找满足精度要求的近似解。也就是说,相对于一般投影法,Krylov子空间法选取了Krylov子空间作为搜索空间
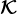 。
。对于线性方程组
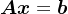 ,Krylov子空间法可以表述为:给定初始解向量
,Krylov子空间法可以表述为:给定初始解向量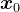 ,令
,令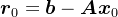 ,选取
,选取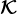 为
为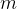 维Krylov子空间,即
维Krylov子空间,即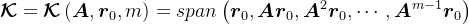 ,寻找
,寻找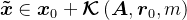 ,使得
,使得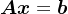 满足Petrov-Galerkin条件,即
满足Petrov-Galerkin条件,即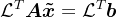 。其中
。其中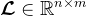 ,选择不同的
,选择不同的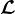 ,就对应不同的Krylov子空间法,
,就对应不同的Krylov子空间法,若设
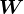 、
、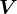 分别是
分别是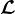 、
、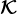 的一组基向量,并令
的一组基向量,并令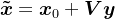 ,则有
,则有 。若
。若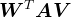 可逆,则有
可逆,则有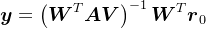 。
。由此可以看出,Krylov子空间法的核心是如何计算
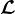 与
与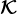 。对于
。对于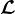 ,目前广泛采用的选取方法如下表,
,目前广泛采用的选取方法如下表,约束空间 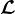
典型方法 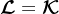
CG 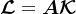
MINRES、GMRES 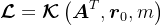
BiCG 4.1 Steepest Descent Method
4.2 Conjugate Gradient Method
下面考虑对称正定线性方程组
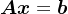 ,其中,
,其中,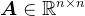 ,
, ,
,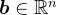 。
。使用Arnoldi分解定理,可得到矩阵
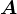 的
的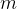 步Arnoldi分解,即
步Arnoldi分解,即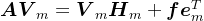 ,其中,
,其中,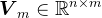 ,
,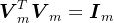 ,
,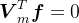 ,
,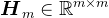 是Hessenberg矩阵,
是Hessenberg矩阵,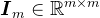 是
是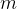 阶单位矩阵,
阶单位矩阵,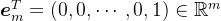 。
。因为
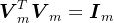 ,
,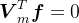 ,可知
,可知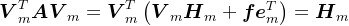 ,由于
,由于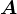 对称,则矩阵
对称,则矩阵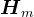 也是对称矩阵,进一步,结合Hessenberg矩阵的定义,可知
也是对称矩阵,进一步,结合Hessenberg矩阵的定义,可知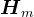 是三对角矩阵。另外,对于
是三对角矩阵。另外,对于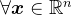 ,则
,则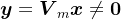 ,此时
,此时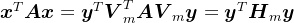 ,由于
,由于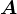 正定,则知0" src="https://latex.csdn.net/eq?%5Cboldsymbol%7By%7D%5E%7BT%7D%5Cboldsymbol%7BH%7D_%7Bm%7D%5Cboldsymbol%7By%7D%3D%5Cboldsymbol%7Bx%7D%5E%7BT%7D%5Cboldsymbol%7BA%7D%5Cboldsymbol%7Bx%7D%3E0" />,即矩阵
正定,则知0" src="https://latex.csdn.net/eq?%5Cboldsymbol%7By%7D%5E%7BT%7D%5Cboldsymbol%7BH%7D_%7Bm%7D%5Cboldsymbol%7By%7D%3D%5Cboldsymbol%7Bx%7D%5E%7BT%7D%5Cboldsymbol%7BA%7D%5Cboldsymbol%7Bx%7D%3E0" />,即矩阵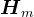 也是正定矩阵。因此,若矩阵
也是正定矩阵。因此,若矩阵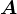 对称正定,矩阵
对称正定,矩阵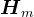 也是对称正定矩阵,更加准确地说,
也是对称正定矩阵,更加准确地说,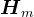 是对称正定三对角矩阵。
是对称正定三对角矩阵。令
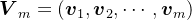 ,并令矩阵
,并令矩阵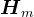 第
第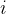 行第
行第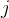 列元素
列元素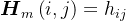 ,则有
,则有 ,考虑到
,考虑到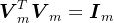 ,因此,可得到Arnoldi分解的递推公式,
,因此,可得到Arnoldi分解的递推公式,![数值线性代数: Krylov子空间法 \left\{\begin{matrix} h_{i,j}=\frac{\mathbf{v}_{i}^{T}\boldsymbol{A}\boldsymbol{v}_{j}}{\boldsymbol{v}_{i}^{T}\boldsymbol{v}_{i}}=\mathbf{v}_{i}^{T}\boldsymbol{A}\boldsymbol{v}_{j}, i\in \left [ 1,j \right ]\\ h_{j+1,j}=\frac{\mathbf{v}_{j}^{T}\boldsymbol{A}\boldsymbol{v}_{j}}{\boldsymbol{v}_{j+1}^{T}\boldsymbol{v}_{j+1}}=\mathbf{v}_{j}^{T}\boldsymbol{A}\boldsymbol{v}_{j}, j\in \left [ 1,m-1 \right ]\\ \boldsymbol{v}_{j+1}= \frac{Av_{j}-\sum_{i=1}^{i=j}h_{i,j}v_{i}}{h_{j+1,j}}, j\in \left [ 1,m-1 \right ]\end{matrix}\right.](https://js.wyfx2014.com/zb_users/upload/2024/03/20240316075815171054709518084.png)
由此,可以看出矩阵
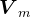 是Krylov子空间
是Krylov子空间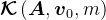 的一组标准正交基。因此,对应于Krylov子空间法,可取
的一组标准正交基。因此,对应于Krylov子空间法,可取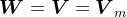 。
。若给定的初始向量
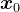 ,令近似解
,令近似解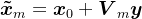 ,根据Petrov-Galerkin条件,有
,根据Petrov-Galerkin条件,有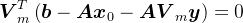 ,记
,记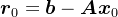 ,则
,则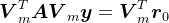 ,结合Arnoldi分解,有
,结合Arnoldi分解,有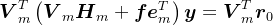 ,考虑到
,考虑到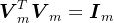 与
与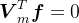 ,即有
,即有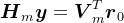 。
。根据Cholesky分解定理,因为
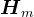 对称正定,则
对称正定,则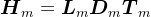 ,其中,矩阵
,其中,矩阵 是下三角矩阵,
是下三角矩阵, 为对角元均为正数的对角矩阵,
为对角元均为正数的对角矩阵,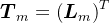 。
。若选取
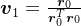 ,则
,则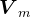 是Krylov子空间
是Krylov子空间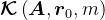 的一组标准正交基,此时
的一组标准正交基,此时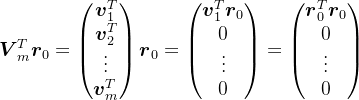
记
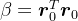 ,
,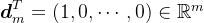 ,则有
,则有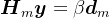 。
。由上述分析,矩阵
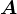 进行
进行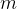 步Arnoldi分解,使用Krylov子空间法,可以得到近似解
步Arnoldi分解,使用Krylov子空间法,可以得到近似解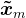 :
: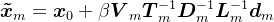 ,其中,
,其中,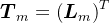 。
。类似地,矩阵
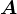 进行
进行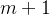 步Arnoldi分解,按照上面地思路,亦可得到近似解
步Arnoldi分解,按照上面地思路,亦可得到近似解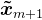 :
: ,其中,
,其中,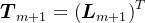 。
。根据Arnoldi分解过程,很明显,
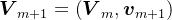 ,
,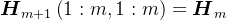 ,
,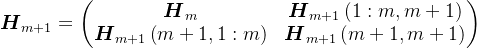 ,
,同时,
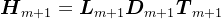 ,并将
,并将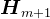 、
、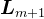 、
、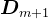 、
、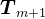 分块,则有
分块,则有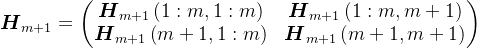
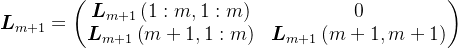
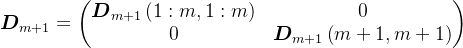
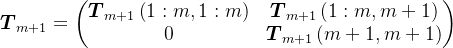
则有,
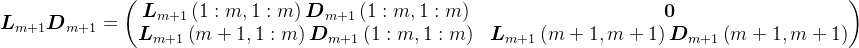
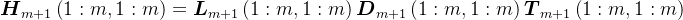
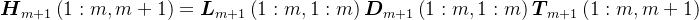
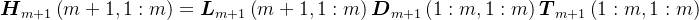
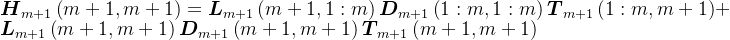
由于
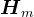 、
、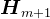 是对称正定三角矩阵,则知
是对称正定三角矩阵,则知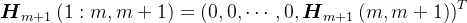 ,
,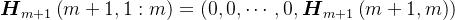 ,
,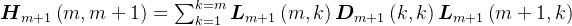 ,
,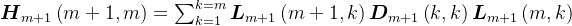
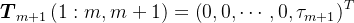 ,
,其中,
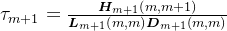 。
。考虑到Cholesky分解的唯一性,则
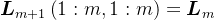 ,
,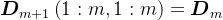 ,
,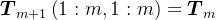 ,即
,即
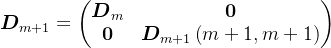


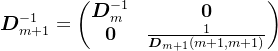
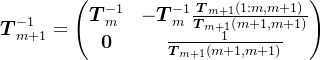
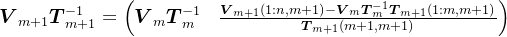
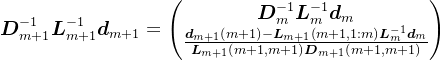
令
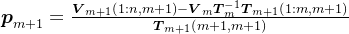 ,
,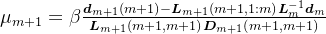
则,
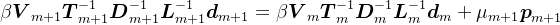 ,
,由上述表达式,可得共轭梯度法中近似解的递推公式:
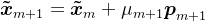
将近似解
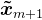 代入原方程组,可得残差向量的递推公式:
代入原方程组,可得残差向量的递推公式: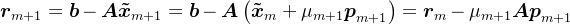
由于
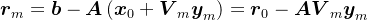 ,将
,将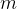 步Arnoldi分解代入,则有
步Arnoldi分解代入,则有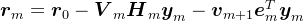 ,其中,
,其中,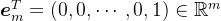 。另外,由于
。另外,由于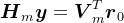 ,则有,
,则有,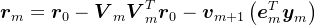 。如前面分析知,
。如前面分析知,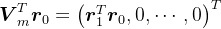 ,所以,
,所以,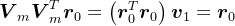 。因此,
。因此,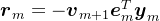 ,也就是说,
,也就是说, 平行于
平行于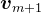 ,且
,且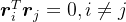 。
。由于
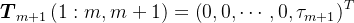 ,则有
,则有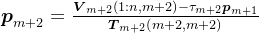 ,也就是说,
,也就是说,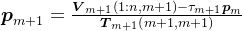 。实际上,
。实际上,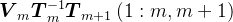 是
是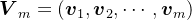 的线性组合,
的线性组合,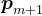 是
是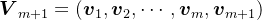 的线性组合。对于
的线性组合。对于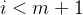 ,
,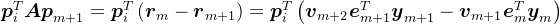 ,根据矩阵
,根据矩阵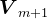 正交性,很容易知道,
正交性,很容易知道,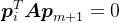 。也就是说,对于
。也就是说,对于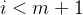 ,向量
,向量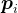 与向量
与向量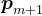 关于矩阵
关于矩阵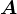 共轭。这其实就是共轭梯度法得名的原因。
共轭。这其实就是共轭梯度法得名的原因。由上述分析,可知,
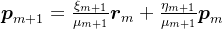 ,其中,
,其中,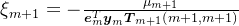 ,
,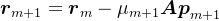 ,
,至此,可以得到简化后的近似解表达式:
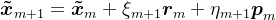
相应地,简化后的的残差向量表达式:

由
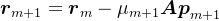 ,可知
,可知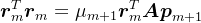 。即
。即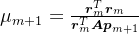 。
。由于
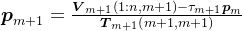 ,可知
,可知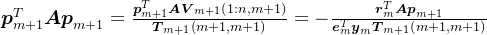 。即
。即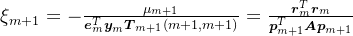 。
。另外,由于
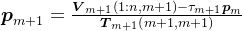 ,可知
,可知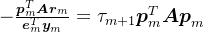 。即
。即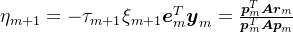 。
。相应地,
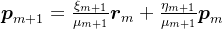 。
。以上即为整个共轭梯度法的推导过程。
4.3 Preconditioned Conjugate Gradient
参考书籍
Golub G H , Loan C F V .Matrix Computations.Johns Hopkins University Press,1996.
Ford W .Numerical Linear Algebra with Applications using MATLAB. 2014.
徐树方. 数值线性代数(第二版). 北京大学出版社, 2010.
参考文献
Hestenes M R , Stiefel E L .Methods of Conjugate Gradients for Solving Linear Systems. Journal of Research of the National Bureau of Standards (United States), 1952.
Arnoldi W E .The principle of minimized iterations in the solution of the matrix eigenvalue problem.Quarterly of Applied Mathematics, 1951, 9(1).
Saad Y .Krylov Subspace Methods for Solving Large Unsymmetric Linear Systems.Mathematics of Computation, 1981, 37(155):105-105.
- 若

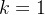 时
时