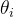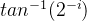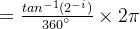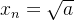一、前言
要理解cordic算法,我们先证明一道中学的数学题。
已知,OA逆时针旋转θ角度后得到OB,线段OA=OB,∠AOB=θ,A 点坐标(x1,y1),B 点坐标(x2,y2)。
求证:
x2=x1*cosθ - y1*sinθ
y2=x1*sinθ+ y1*cosθ
证明:
如图所示,假设A在第一象限,点A沿着点O做旋转至点B,可能旋转到第一象限或者第二象限或者第三象限或者第四象限。假设OA=OB=m。
假设点B在第一象限,求证如下:
根据三角函数定理:x1=m*cosα,y1=m*sinα。
x2=m*cos(α+θ)=m*(cosαcosθ- sinαsinθ)
=m*(cosαcosθ- cosαtanαsinθ)
=m*cosα*(cosθ- tanαsinθ)
=x1*(cosθ- tanαsinθ)
=x1*cosθ-x1* tanαsinθ
=x1*cosθ-y1* sinθ
y2=m*sin(α+θ)=m*(sinαcosθ+ cosαsinθ)
=m*sinαcosθ+ m*cosαsinθ)
=y1cosθ+x1sinθ
题目得证。
假设点B在第四象限,求证如下:
根据三角函数定理:x1=m*cosα,y1=m*sinα。
x2=m*cos(360°-(θ+α))=m*cos(-(α+θ))=
=m*cos(α+θ)=m*(cosαcosθ- sinαsinθ)
=m*(cosαcosθ- cosαtanαsinθ)
=m*cosα*(cosθ- tanαsinθ)
=x1*(cosθ- tanαsinθ)
=x1*cosθ-x1* tanαsinθ
=x1*cosθ-y1* sinθ
y2=-m*sin(360°-(θ+α))=-m*sin(-(θ+α))
=m*sin(α+θ)=m*(sinαcosθ+ cosαsinθ)
=m*sinαcosθ+ m*cosαsinθ)
=y1cosθ+x1sinθ
题目得证。
实际上,使用同样的方法可以证明,无论A在第几象限,B旋转到第几象限,该公式都成立。
二、CORDIC算法基本原理
2.1 CORDIC算法的初步推理
由上述证明可以了解到,OA旋转θ角度后得到OB,A 点坐标(x1,y1),B 点坐标(x2,y2),A点和B点之间的关系为:x2=x1*cosθ - y1*sinθ;y2=x1*sinθ+ y1*cosθ
为了方便书写和观察,上述公式写成矩阵的形式:
好了,现在我们根据这个证明的公式,进行下一步的算法推导。
假设有一点(x1,y1),第一次旋转了到B点(x2,y2),B点坐标可以表示为:
第二次旋转了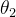 到C点(x3,y3),C点坐标可以表示为:
到C点(x3,y3),C点坐标可以表示为:
那么第i次旋转到Z点(xi+1,yi+1),Z点坐标可以表示为:
提取出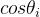 转化为:
转化为:
这样就得到了初步的Cordic算法公式:
或者
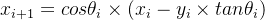
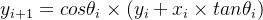
2.2 CORDIC算法的再次转换
2.2.1先分析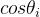
为了方便计算,把上述公式调整为
即忽略掉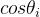 ,对于某个固定的旋转角度,为常数。忽略掉带来的后果是,每旋转1次,得到的横坐标x和纵坐标y各缩放了。但是这样做的好处是减少了一部分余弦运算和乘法运算,非常方便硬件实现。
,对于某个固定的旋转角度,为常数。忽略掉带来的后果是,每旋转1次,得到的横坐标x和纵坐标y各缩放了。但是这样做的好处是减少了一部分余弦运算和乘法运算,非常方便硬件实现。
我们将x和y坐标缩放了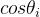 的旋转过程称为伪旋转,角度正确但是模长变为原来的
的旋转过程称为伪旋转,角度正确但是模长变为原来的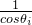 。
。
忽略掉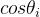 后,只需要计算
后,只需要计算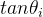 ,就可以得到旋转后的伪坐标 。
,就可以得到旋转后的伪坐标 。
当然,获得正确的坐标是需要乘上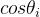 的,这个我们在后面会有讨论。
的,这个我们在后面会有讨论。
2.2.2再分析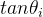
使用cordic算法,适用于FPGA设计时,我们固定取第i(一般硬件是从0开始计数)次旋转的角度为。为什么固定取这个角度值呢?根据公式
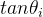 为乘数,需要与xi与yi相乘,而硬件比较容易通过移位实现2的乘法和除法,因此此处最好取值为2的幂。可以参考下表。按照经验一般旋转16次就可以得到比较精确的逼近值。
为乘数,需要与xi与yi相乘,而硬件比较容易通过移位实现2的乘法和除法,因此此处最好取值为2的幂。可以参考下表。按照经验一般旋转16次就可以得到比较精确的逼近值。
| 第i次旋转(从0开始计数) | 旋转角度 | 旋转弧度 | |
| 0 | 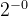 | 45° | 0.78539 |
| 1 | 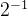 | 26.565° | 0.46365 |
| 2 | 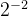 | 14.036° | 0.24498 |
| 3 | 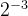 | 7.1250° | 0.12435 |
| 4 | 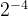 | 3.5763° | 0.06241 |
| 5 | 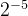 | 1.7899° | 0.03123 |
| 6 | 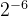 | 0.8951° | 0.01562 |
| 7 | 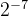 | 0.4476° | 0.00781 |
| 8 | 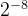 | 0.2238° | 0.00391 |
| 9 | 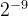 | 0.1119° | 0.00195 |
| 10 | 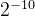 | 0.0559° | 0.00098 |
| 11 | 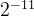 | 0.0279° | 0.00049 |
| 12 | 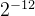 | 0.0139° | 0.00024 |
| 13 | 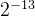 | 0.0069° | 0.00012 |
| 14 | 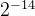 | 0.0035° | 0.00006 |
| 15 | 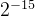 | 0.0017° | 0.00003 |
| ... | ... | ... | ... |
| i | 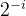 |
|
|
即在每次旋转中,限定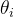 取某些限定的数值,使:
取某些限定的数值,使:
第0次旋转,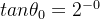
第1次旋转,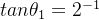
第2次旋转,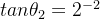
第3次旋转,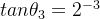
......
第i次旋转,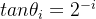
根据公式:
该公式可以表示成下面的形式:
也可以表示下面的形式:
每次计算的时候,只需要除以2、除以4、除以8等一系列运算,还有一些加减法运算而已。而除以2的幂可以使用数据按位右移实现,因此非常容易用硬件实现。
但是在旋转的过程中,使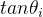 等于2的幂的方式,可能会带来两个问题。
等于2的幂的方式,可能会带来两个问题。
a、朝着目标角度进行旋转时,可能会出现没有超过目标角度的情况,当然也存在超过目标角度的情况,而我们迭代旋转的目的时要逼近目标角度,通过多次旋转,逐渐旋转到目标角度,因此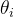 有可能是逆时针旋转也有可能是顺时针旋转。
有可能是逆时针旋转也有可能是顺时针旋转。
如下图所示:
根据这个图可以看到:
第0次旋转时,逆时针旋转45°
第1次旋转时,逆时针旋转26.6°
第2次旋转时此时因为前两次旋转的角度大于60°,因此此次顺时针旋转了14°
依次类推。
因此我们需要将公式进行优化,优化为
即
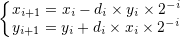
di为旋转方向的旋转因子,逆时针旋转时di=1,顺时针时di=-1。
那么如何判断是否旋转到了目标位置内呢? 此时引入了角度累加器的概念。
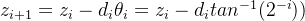
其中表示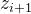 第i次旋转后的角度累加器的值,即距离目标位置的角度值。 zi大于0时,di=1,反之,di=-1。还是使用上图的例子,目标角度是60°。
第i次旋转后的角度累加器的值,即距离目标位置的角度值。 zi大于0时,di=1,反之,di=-1。还是使用上图的例子,目标角度是60°。
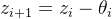
z为距离目标位置剩余的旋转角度。z0默认为θ,表示还未旋转时,距离目标位置的角度为θ。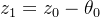 ,表示第一次旋转式,旋转了角度
,表示第一次旋转式,旋转了角度 ,距离目标位置的距离为
,距离目标位置的距离为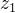 ,即
,即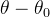 ,以此类推。
,以此类推。
第0次旋转时旋转45°,z0=60°,d0=1,因此进行逆时针旋转,z1=60°-45°=15°,此时距离目标角度15°,d1=1;
第1次旋转时旋转26.6°,z1=15°,d1=1,因此进行逆时针旋转,z2=15°-26.6°=-11.6°,此时距离目标角度-11.6°,d2=-1,下次旋转需要进行顺时针旋转;
第2次旋转时旋转14°,因为z2=-11.6°,d2=-1°,顺时针旋转后,z3=-11.6°+14°=2.4°,此时距离目标角度2.4°,d3=1,下次旋转需要进行逆时针旋转;
依次类推。
因为θ的角度值固定,我们可以提前计算出来保存在RAM或者查找表中,一般保存16次旋转的角度值即可。在角度累加的时候,通过比较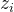 数值的正负,来判断下一次的计算角度累加器时di的正负。当然,也可以直接比较目前累加或者累减的角度至与目标角度值的大小关系,来判断下一次应该时加法还是减法。
数值的正负,来判断下一次的计算角度累加器时di的正负。当然,也可以直接比较目前累加或者累减的角度至与目标角度值的大小关系,来判断下一次应该时加法还是减法。
b、因为θ的取值从45°、26.6°、14°依次累加或者累减,参考资料了解到其旋转角度的范围为(-99.88°,99.88°)。若初始角度为0°,则可以认为目标角度只能在第一象限和第四象限。若需要旋转到第二和第三象限,需要进行预处理。如何进行预处理呢?
首先,旋转最大和最小角度的计算:
至于怎么进行预处理,只需要根据之前证明的公式:进行三角函数转化即可。
首先上面计算的,为了方便三角函数的计算,当旋转角度在(-90°,90°)的范围内时无需进行预处理,当超过这个角度时,就需要进行三角函数转换进行预处理。
坐标处于第二象限:
假设旋转的β角度范围是(90°,180°)(初始位置在x正半轴时,逆时针旋转,此角度处于第二象限),α=β-90°的取值范围是(0,90°)。我们的目的是,将第二象限的坐标信息用第一象限的坐标信息进行表述,这样就可以利用tanθ是2的幂的优势,位移计算。假设A’点坐标(x1’,y1’),处于第一象限;A点坐标(x1,y1),处于第二象限,二者夹角为β-α=90°,由B到A为顺时针旋转预处理转化过程:
这样A点(x1,y1)用A’点(x1’,y1’)就可以表示出来,A’(y1’,-x1’)。我们计算出A’点坐标和角度,就可以变相计算出A点坐标和角度。
坐标处于第三象限:
假设β的角度范围是(180°,270°),即(-180°,-90°)(初始位置在x正半轴时,逆时针旋转,此角度处于第三象限),α=β+90°的取值范围是(-90°,0°)。我们的目的是,将第三象限的坐标信息用第四象限的坐标信息进行表述,这样就可以利用tanθ是2的幂的优势,位移计算。假设B’点坐标(x2’,y2’),处于第四象限,B点坐标(x2,y2),处于第三象限,二者夹角为β-α=-90°由B到A为逆时针旋转,预处理转化过程:
假设B点坐标是固定的(x2,y2),则预处理后坐标为B’(y2,-x2)。这样B点(x2,y2)用B’点(x2’,y2’)用就可以表示出来,B(-y2’,-x2’)。我们计算出A点坐标和角度,就可以变相计算出B点坐标和角度。
预处理方式和结果列表如下:
| 目标坐标 | 目标旋转角度(范围) | 预处理旋转 | 预处理后坐标结果 | 预处理后旋转角度 | 备注 |
| (x,y) | θ(0°,90°) | 0° | (x,y) | θ | / |
| (x,y) | θ(90°,180°) | 90° | (-y,x) | θ-90° | / |
| (x,y) | θ(180°,270°) | -90° | (y,-x) | θ+90° | / |
| (x,y) | θ(270,90°) | 0° | (x,y) | θ | / |
预处理完成后,然后再按照上述描述的缩放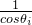 ,然后将tan表示为2的幂的方式进行累加逼近即可,计算出预处理的计算坐标后,再按照上述表格转化出实际的目标坐标。此处不再多言。
,然后将tan表示为2的幂的方式进行累加逼近即可,计算出预处理的计算坐标后,再按照上述表格转化出实际的目标坐标。此处不再多言。
2.2.3 cosθ的还原补偿
前面分析cosθ时讲到了伪旋转,每旋转1次,缩放了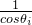 ,那么我们最终要恢复原有的模长度的话,就需要在最后将之前缩放的比例再进行还原。如何还原呢?
,那么我们最终要恢复原有的模长度的话,就需要在最后将之前缩放的比例再进行还原。如何还原呢?
计算出每次旋转时的 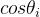 ,累乘即可。
,累乘即可。
之前我们分析tanθ时,推导出:
那么现在我们假设每次旋转的伸缩系数为Ki=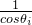 ,那么我们的补偿系数就应该为Ai=
,那么我们的补偿系数就应该为Ai=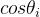 。则补偿后的坐标值(或者称为准确坐标)为。
。则补偿后的坐标值(或者称为准确坐标)为。
因为分析tanθ时,我们知道,,那么,进行推导如下:
计,那么旋转n次,总的伸缩因子,补偿因子
我们知道,旋转的次数越多,数值越小。当旋转次数n趋近于无穷大时,趋近于0。而cos(0°)=1,cos函数在(0,90°)范围内递减,因此,在旋转无穷多次时趋近于1。经过计算,可以得出,当n趋于无穷大时,A趋近于0.607252935,K趋近于1.646760258。(基本旋转16次之后,K值基本不发生变化,与前面tanθ的旋转角度越来越精确相呼应)
当旋转次数n趋近于无穷大时,那么目前旋转的角度值无限接近于目标坐标的角度值
可以表述为
其中(x0,y0)为初始坐标位置,(xi+1,yi+1)近似为目标位置坐标。
当然,该公式在旋转16次左右的时候也可认为成立,毕竟误差已经非常小。
2.2.4 CORDIC算法公式推导结论
前面推理了很多,现在把前面所有推理的内容整合一下,方便用硬件实现的CORDIC算法的公式如下:
我们设计实现的时候,通过迭代的方式,每次旋转的角度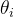 是已知的,一般只迭代16次,因此和的具体数值可以实现存放在查找表或者ROM中,使用的时候直接提取即可。
是已知的,一般只迭代16次,因此和的具体数值可以实现存放在查找表或者ROM中,使用的时候直接提取即可。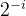 可以直接使用移位实现;di可以通过比较目标角度值与
可以直接使用移位实现;di可以通过比较目标角度值与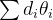 的大小关系判断正负,当然也可以直接判断zi(zi大于0时,di=1,反之di=-1)判断正负。
的大小关系判断正负,当然也可以直接判断zi(zi大于0时,di=1,反之di=-1)判断正负。
每次迭代需要2次移位操作(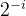 为移位操作,x,y各需要1次移位操作),2次ROM查找表(查找
为移位操作,x,y各需要1次移位操作),2次ROM查找表(查找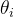 的角度值,
的角度值,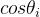 数值),3次加减法(x,y,z各1次加法,加法还是减法由di判断)。2次乘法(x,y的坐标补偿数值)。
数值),3次加减法(x,y,z各1次加法,加法还是减法由di判断)。2次乘法(x,y的坐标补偿数值)。
当然,因为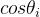 的累乘数值在迭代16次后,无限接近于0.607252935,因此我们也可以直接把
的累乘数值在迭代16次后,无限接近于0.607252935,因此我们也可以直接把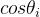 的累乘数值直接赋值,省去这部分的ROM,并且所有的迭代只需要执行2次乘法即可(x,y各1次)。公式可以直接表示为:
的累乘数值直接赋值,省去这部分的ROM,并且所有的迭代只需要执行2次乘法即可(x,y各1次)。公式可以直接表示为:
三、CORDIC的几种模式
根据CORDIC算法的模式,就可以使用硬件逻辑计算不同的运算符了。目前我这边主要希望使用CORDIC算法计算cos/sin/角度值/平方根这四种运算,对应着旋转模式、向量模式、双曲模式,以下分别讨论。
3.1旋转模式
旋转模式:已知一个坐标点(x0,y0),旋转一个角度值θ。
利用旋转模式可以求得cos值与sin值。此时只需要角度正确即可,不需要进行模长补偿。
直接使用公式:
在旋转模式中,di与zi符号相同,即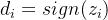 ,zi为第i次旋转时,距离目标坐标的角度值。
,zi为第i次旋转时,距离目标坐标的角度值。
n次(n->∞)迭代后可以得到:
上述公式可以这么理解:
那么我们如何求得cos值呢?根据等式:
当取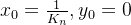 时,带入xn,得到
时,带入xn,得到
此时回到硬件实现上,我们知道,当取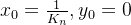 时,可以求解cos和sin的计算,,硬件实现时,使用公式
时,可以求解cos和sin的计算,,硬件实现时,使用公式
3.2向量模式
向量模式:已知一个坐标点(x0,y0),把他旋转到x轴(xn,0)。
在向量模式中,旋转方向的选择di与xi*yi的符号相反,即,一直旋转到yi趋近于0。
由定义我们知道,初始坐标的模长为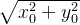 ,经过n次伪旋转,旋转到(xn,0)坐标时:
,经过n次伪旋转,旋转到(xn,0)坐标时:
由此可以得到:当取x0=1时,可以得到:
由此可以计算出初始坐标(x0,y0)所对应的角度值zn。
3.3其余坐标系引入以及总结
前面的旋转模式、向量模式都是基于圆周坐标系的基础上得到的,为了能计算更多不同的函数,比如平方根、双曲正弦函数、双曲余弦函数等,引入了线性旋转模式和双曲线旋转模式两种模式。为了计算平方根函数,我们再研究一下双曲旋转模式。
当不在圆周上旋转时,经过计算引入了新的旋转模式,线性旋转和双曲旋转,这里也不详细学习概念性的东西了,也不再研究公式的推导过程,直接理解使用。
通用公式如下(包含圆周旋转、线性旋转、双曲旋转):
双曲旋转时,有几点与圆周旋转不同:
1、双曲旋转时,由于i取0时,tan-1(2^0)为∞,z1+1=z0-d0tan-1(2^0),无法计算,因此i从1开始。并且i的取值不是递增,而应该从曲线收敛的角度进行考虑,从i=4,i=13,等满足i=3i+1(下一次需要重复的i,为本次重复的序号的3倍+1)时,该次迭代必须重复,才能保证收敛。从而迭代过程变为i=1,2,3,4,4,5,6,7,8,9,10,11,12,13,13,14,15......
2、当使用双曲旋转时,模长的伸缩因子与圆周旋转有所不同,其伸缩因子计算公式如下:
(根据i = 1 ,2 ,3 ,4 , 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 13, 14, 15累乘计算,我们可以计算得到Kn趋近于0.82815936)
据此我们还可以知道,限定了在双曲旋转时,z的取值范围时[-1.1181,1.1181],在向量模式下,y1/x1的取值范围为[-0.8069,0.8069]。
| 旋转模式 | 向量模式
| 备注 | |
| 圆周旋转 | 已知初始坐标(x0,y0)和以及其与目标坐标的角度值z0,可以得到伪旋转后的目标坐标。取x0=1/K,y0=0,就可以求得cosz0和sinz0数值 | 已知初始坐标(x0,y0)和以及其与目标坐标的角度值z0,向横坐标x轴旋转,可以得到伪旋转后的目标坐标(xn,0)。取x0=1,z0=0,就可以求得n次旋转的累加角度值,也即是 | |
| 线性旋转 | 取y0=0,则n次旋转之后yn=x0*z0,就可以依据此公式计算乘法值。 | 取z0=0,则n次旋转之后zn=y0/x0,就可以依据此公式计算除法值。 | |
| 双曲旋转 | 与圆周旋转类似,取x0=1/K',y0=0,就可以求得cosh(z0)和sinh(z0)数值 | 与圆周旋转类似,取x0=1,z0=0,就可以求得。 另外,当需要算数值a的平方根时,可以令x0=a+1/4,y0=a-1/4,带入可得 |
四、CORDIC算法还能干什么?
我们研究CORDIC算法的目的,就是在实际工程应用中使用该算法实现方便的计算。那么,CORDIC算法都能做什么呢?
前面我们了解到,CORDIC算法可以算得.
- 乘除法
- 余弦cos
- 正弦sin
- 直角坐标与角度的互相转换
- 平方根
- 双曲线函数。
除此之外,还可间接获得以下函数
- tanz(tanz=sinz/cosz)
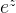 函数、(
函数、(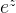 =coshz+jsinhz)
=coshz+jsinhz)- 指数函数
....
后面有需要的时候再行研究,此处不再深入学习了。