用斐波那契数列感受算法的神奇（21亿耗时0.02毫秒）

分类:热门推荐日期:2024-05-01浏览:1评论:0

目录

一、回顾斐波那契数列

二、简单递归方法

（一）解决思路

（二）代码展示

（三）性能分析

三、采用递归+HashMap缓存

（一）解决思路

（二）代码展示

（三）性能分析

四、采用递归+数组缓存（记忆化搜索）

（一）解法思路

（二）代码展示

（三）性能分析

五、数组缓存+顺序迭代

（一）解法思路

（二）代码展示

（三）性能分析

六、取消缓存直接采用迭代优化

（一）解法思路

（二）代码展示

（三）性能分析

七、用初等代数推导公式解法

（一）解法分析

（二）代码展示

（三）性能分析

八、矩阵解法

（一）解法分析

（二）代码展示

（三）性能分析

九、矩阵解法+快速幂

（一）解法分析

（二）代码展示

（三）性能分析

十、最优解分析

针对斐波那契数列算法进行详细介绍和优化，从最简单的递归方法到更高效的迭代、缓存、动态规划、公式推导和矩阵解法，最终达到了时间复杂度为O(logn)的快速幂矩阵解法来感受算法的神奇之处，最后可以看到如何实现在输入n=2100000000（21亿）时仅耗时0.02毫秒的最佳效果。

一、回顾斐波那契数列

斐波那契数列（Fibonacci sequence）是一种非常经典的数学序列，其特点是每个数字是前两个数字之和，起始于0和1。也就是说，数列的第三个数是前两个数的和，第四个数是第二个数和第三个数的和，以此类推。斐波那契数列的前几项是：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

这个数列最早是意大利数学家斐波那契（Fibonacci）在其《算盘书》（1202年）中引入的，用来描述兔子繁殖的理想化情况。假设一对刚出生的兔子一年后成熟并能生育，且从第二年开始每年产下一对新兔子，不考虑其他因素的影响。这个问题导致了斐波那契数列的产生，兔子的对数就对应了斐波那契数列的每一项。

那通过算法实现求第n个斐波那契数的具体数值，让我们感受下算法的不断优化和极致表现。

二、简单递归方法

（一）解决思路

递归的思路是将一个大问题拆解成更小的相似问题来解决。

对于斐波那契数列，我们首先要考虑斐波那契数列的基本情况，即当n为0或1时，斐波那契数列的值分别为0和1。这是递归的结束条件。

接下来，我们需要定义斐波那契数列的递归关系。根据定义，斐波那契数列的第n个数是前两个数之和，即F(n) = F(n-1) + F(n-2)。因此，我们可以将问题拆解成求解F(n-1)和F(n-2)的问题。

在求解F(n)之前，我们需要先求解F(n-1)和F(n-2)。为了求解这两个问题，我们可以再次调用相同的函数，直到达到基本情况。

在递归调用的过程中，当n为0或1时，递归将会终止。这是因为这两个值是斐波那契数列的基本情况，不需要再进行递归调用。

但需要注意的是，递归方法在求解大规模斐波那契数列时效率非常低，因为存在大量的重复计算。因此，虽然递归是一种常用的解决问题的方法，但在实际应用中需要谨慎使用，尤其是在处理大规模数据时。

（二）代码展示

package org.zyf.javabasic.algorithm;
/**
 * @program: zyfboot-javabasic
 * @description: Fibonacci算法
 * @author: zhangyanfeng
 * @create: 2024-04-24 08:22
 **/
public class RecursiveFibonacci {
    /**
     * 当传入n=50时，递归方法在电脑上耗时高达35.549秒。
     */
    public static int fibonacciRecursive(int n) {
        // 边界条件：当n为0或1时，斐波那契数列的值分别为0和1
        if (n == 0) {
            return 0;
        } else if (n == 1) {
            return 1;
        }
        // 递归调用：求解F(n-1)和F(n-2)，然后返回它们的和
        else {
            return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
        }
    }
    public static void main(String[] args) {
        System.out.println("简单递归方法验证");
        // 验证斐波那契数列前几项的正确性
        // 测试不同n值下的性能
        for (int n = 0; n <= 50; n += 5) {
            long startTime = System.nanoTime();
            int result = fibonacciRecursive(n);
            long endTime = System.nanoTime();
            long duration = (endTime - startTime) / 1000000; // 毫秒
            System.out.println("Fibonacci(" + n + ") = " + result + ", Time: " + duration + "ms");
        }
    }
}

（三）性能分析

  1. 时间复杂度：时间复杂度可以近似为O(2^n)，因为每次调用都会分解为两个递归调用，直到达到基本情况。随着n的增加，计算时间呈指数级增长。

  2. 空间复杂度：对于斐波那契数列的递归方法，空间复杂度可以近似为O(n)，因为递归调用栈的深度最多为n。

实际性能验证：当传入n=50时，耗时为37021毫秒，即37.021秒。因此，我们可以合理推测，当传入n=100时，耗时可能会更长，但具体的时间取决于计算机性能和实现细节。（前提：我电脑的配置较高，如果电脑不给力，可能时间更长）

三、采用递归+HashMap缓存

（一）解决思路

采用递归+HashMap缓存的优化方法，也称为Memoization，是一种动态规划的思想。

首先使用递归来求解斐波那契数列的时候，我们知道递归是一种自顶向下的方法，从原始问题开始，不断地将其分解为更小的子问题，直到达到基本情况。

所以在递归的过程中，我们会遇到大量的重复计算。例如，在计算F(5)时，可能会需要计算F(4)和F(3)，而在计算F(4)时又会需要计算F(3)和F(2)，以此类推。

为了避免重复计算，我们可以使用HashMap来缓存已经计算过的结果。这样，当我们需要计算某个斐波那契数时，首先检查HashMap中是否已经存在该值，如果存在则直接返回缓存的结果，否则进行计算并将结果存入HashMap中。

将递归方法转化为自顶向下的动态规划。通过缓存已经计算过的结果避免了重复计算，大大提高了效率。

（二）代码展示

package org.zyf.javabasic.algorithm;
import com.google.common.collect.Maps;
import java.math.BigInteger;
import java.util.HashMap;
/**
 * @program: zyfboot-javabasic
 * @description: 采用递归+HashMap缓存
 * @author: zhangyanfeng
 * @create: 2024-04-24 08:43
 **/
public class MemoizationFibonacci {
    private static HashMap memoization = Maps.newHashMap();
    public static BigInteger fibonacciWithMemoization(int n) {
        if (n <= 1) {
            return BigInteger.valueOf(n);
        }
        // 如果HashMap中已经有了斐波那契数列的第n项的值，则直接返回缓存结果
        if (memoization.containsKey(n)) {
            return memoization.get(n);
        }
        // 如果HashMap中没有斐波那契数列的第n项的值，则进行递归计算，并将结果存入HashMap中
        BigInteger result = fibonacciWithMemoization(n - 1).add(fibonacciWithMemoization(n - 2));
        memoization.put(n, result);
        return result;
    }
    public static void main(String[] args) {
        // 验证斐波那契数列前几项的正确性
        for (int i = 0; i < 10; i++) {
            System.out.println("Fibonacci(" + i + ") = " + fibonacciWithMemoization(i));
        }
        long startTime = System.currentTimeMillis();
        BigInteger result = fibonacciWithMemoization(8000);
        long endTime = System.currentTimeMillis();
        long elapsedTime = endTime - startTime;
        System.out.println("Fibonacci( 8000 ) = " + result);
        System.out.println("程序运行时间：" + elapsedTime + " 毫秒");
        long startTime1 = System.currentTimeMillis();
        BigInteger result1 = fibonacciWithMemoization(10000);
        long endTime1 = System.currentTimeMillis();
        long elapsedTime1 = endTime1 - startTime1;
        System.out.println("Fibonacci(10000) = " + result1);
        System.out.println("程序运行时间：" + elapsedTime1 + " 毫秒");
        long startTime2 = System.currentTimeMillis();
        BigInteger result2 = fibonacciWithMemoization(19000);
        long endTime2 = System.currentTimeMillis();
        long elapsedTime2 = endTime2 - startTime2;
        System.out.println("Fibonacci(19000) = " + result1);
        System.out.println("程序运行时间：" + elapsedTime2 + " 毫秒");
    }
}

（三）性能分析

  1. 时间复杂度：递归+HashMap缓存方法通过缓存已经计算过的结果，避免了重复计算，因此实际的递归调用次数会显著减少。时间复杂度是优化后的O(n)，其中n是斐波那契数列的索引。

  2. 空间复杂度：使用HashMap来存储已经计算过的斐波那契数列的值。因此空间复杂度主要取决于递归调用的深度，空间复杂度是O(n)。

实际运行发现当n为8000耗时6 毫秒，n为10000时耗时1毫秒，性能变好了，但当n为18000的时候耗时4毫秒性能上又变差了，然后n为18400时出现StackOverflowError。性能上破不了18400。

递归的调用栈是有限的，因此当递归层级过深时会导致 java.lang.StackOverflowError。在斐波那契数列问题中，使用递归求解时，随着n的增大，递归调用的层级也会线性增长，因此当n较大时，容易出现栈溢出的情况。

为了解决这个问题，可以考虑使用迭代的方式来计算斐波那契数列，而不是递归。迭代的方式不会涉及到递归调用，因此不会出现栈溢出的情况，适用于大规模的计算。

四、采用递归+数组缓存（记忆化搜索）

（一）解法思路

采用递归+数组缓存的方法是一种记忆化搜索（Memoization）或者自顶向下的动态规划的经典应用。核心思想是通过递归的方式计算斐波那契数列的值，并利用数组来缓存已经计算过的值，避免重复计算，从而提高效率。

首先定义一个递归函数，用来计算斐波那契数列的第n项的值。在递归函数中，需要处理两种情况：

  • 基本情况：当n为0或1时，直接返回n作为结果。
  • 递归情况：对于其他的n，递归地计算斐波那契数列的第n-1项和第n-2项的值，然后将它们相加作为结果返回。

    在递归函数中，使用一个数组来缓存已经计算过的斐波那契数列的值。每次计算新的斐波那契数列的值之前，先检查数组中是否已经存在了对应项的值。如果存在，则直接返回缓存结果，而不进行重复计算；如果不存在，则进行递归计算，并将结果存入数组中。在递归函数的最后，返回计算得到的斐波那契数列的第n项的值。

    （二）代码展示

    package org.zyf.javabasic.algorithm;
import java.math.BigInteger;
/**
 * @program: zyfboot-javabasic
 * @description: 采用递归+数组缓存的方法来计算斐波那契数列
 * @author: zhangyanfeng
 * @create: 2024-04-24 23:22
 **/
public class MemoizationFibonacciForArray {
    private static BigInteger[] memoization;
    public static BigInteger fibonacciWithMemoization(int n) {
        memoization = new BigInteger[n + 1]; // 初始化缓存数组
        return fib(n);
    }
    private static BigInteger fib(int n) {
        if (n <= 1) {
            return BigInteger.valueOf(n);
        }
        // 如果缓存中已经有了斐波那契数列的第n项的值，则直接返回缓存结果
        if (memoization[n] != null) {
            return memoization[n];
        }
        // 如果缓存中没有斐波那契数列的第n项的值，则进行递归计算，并将结果存入缓存数组中
        memoization[n] = fib(n - 1).add(fib(n - 2));
        return memoization[n];
    }
    public static void main(String[] args) {
        int n1 = 10000;
        long startTime1 = System.currentTimeMillis();
        BigInteger result1 = fibonacciWithMemoization(n1);
        long endTime1 = System.currentTimeMillis();
        long elapsedTime1 = endTime1 - startTime1;
        System.out.println("Fibonacci(" + n1 + ") = " + result1);
        System.out.println("程序运行时间：" + elapsedTime1 + " 毫秒");
        int n2 = 15000;
        long startTime2 = System.currentTimeMillis();
        BigInteger result2 = fibonacciWithMemoization(n2);
        long endTime2 = System.currentTimeMillis();
        long elapsedTime2 = endTime2 - startTime2;
        System.out.println("Fibonacci(" + n2 + ") = " + result2);
        System.out.println("程序运行时间：" + elapsedTime2 + " 毫秒");
        int n3 = 18000;
        long startTime3 = System.currentTimeMillis();
        BigInteger result3 = fibonacciWithMemoization(n3);
        long endTime3 = System.currentTimeMillis();
        long elapsedTime3 = endTime3 - startTime3;
        System.out.println("Fibonacci(" + n3 + ") = " + result3);
        System.out.println("程序运行时间：" + elapsedTime3 + " 毫秒");
    }
}

    （三）性能分析

    1. 时间复杂度：计算斐波那契数列的第n项需要计算前面的n-1项和n-2项，每一项的计算都需要常数时间，因此时间复杂度为O(n)。在递归方法中，对于每个n，我们最多只需计算一次，然后将结果存入缓存数组中，之后再次需要计算时直接从缓存中取值，不再进行重复计算。因此，整个递归过程的时间复杂度为O(n)。

    2. 空间复杂度：在递归方法中使用了一个长度为n+1的数组来存储斐波那契数列的值，因此空间复杂度为O(n+1)，即O(n)。此外，递归调用时的函数调用栈也会占用一定的空间，其空间复杂度取决于递归的最大深度。在这种情况下，最大深度为n，因此额外的空间复杂度也为O(n)。综合起来，整个算法的空间复杂度为O(n)。

    实际运行发现当n为10000耗7毫秒，n为15000时耗时4毫秒，性能变好了，但当n为18000的时候耗时7毫秒性能上又变差了，然后n为18100时出现StackOverflowError。性能比采用递归+HashMap缓存方式还差一些。原因还是递归的调用栈是有限的，性能上破不了18100。

    五、数组缓存+顺序迭代

    （一）解法思路

    数组缓存+顺序迭代，结合了动态规划的思想和迭代的方式来计算斐波那契数列。

    • 首先初始化一个数组，用来存储斐波那契数列的值。数组的长度至少为n+1，以存储从0到n的所有斐波那契数列的值。将斐波那契数列的前两项初始化为0和1，并将其存入数组中。
    • 从第三项开始，通过迭代的方式依次计算斐波那契数列的每一项的值。对于第i项，可以通过前两项的值相加得到，然后将计算得到的值存入数组中。
    • 在计算完成后，数组中的最后一项即为所求的斐波那契数列的第n项的值，将其作为结果返回即可。

      其核心是利用数组来存储已经计算过的斐波那契数列的值，并通过顺序迭代的方式逐步计算下一项的值，由于是顺序迭代计算，不需要额外的函数调用栈空间，因此效率更高。

      （二）代码展示

      package org.zyf.javabasic.algorithm;
import java.math.BigInteger;
/**
 * @program: zyfboot-javabasic
 * @description: 使用数组缓存+顺序迭代方法来计算斐波那契数列
 * @author: zhangyanfeng
 * @create: 2024-04-24 23:42
 **/
public class IterativeArrayFibonacci {
    public static BigInteger fibonacci(int n) {
        if (n <= 1) {
            return BigInteger.valueOf(n);
        }
        // 初始化数组缓存
        BigInteger[] fib = new BigInteger[n + 1];
        fib[0] = BigInteger.ZERO;
        fib[1] = BigInteger.ONE;
        for (int i = 2; i <= n; i++) {
            // 顺序迭代计算每一项的值
            fib[i] = fib[i - 1].add(fib[i - 2]);
        }
        // 返回斐波那契数列的第n项的值
        return fib[n];
    }
    public static void main(String[] args) {
        int[] nValues = {10000, 15000, 20000,30000,40000,10000000};
        for (int n : nValues) {
            long startTime = System.currentTimeMillis();
            BigInteger result = fibonacci(n);
            long endTime = System.currentTimeMillis();
            long elapsedTime = endTime - startTime;
            System.out.println("Fibonacci(" + n + ") = " + result);
            System.out.println("程序运行时间：" + elapsedTime + " 毫秒");
        }
    }
}

      （三）性能分析

      1. 时间复杂度：计算斐波那契数列的第n项时，需要顺序计算从第2项到第n项的所有值。在每次计算时，只需对前两项进行一次加法操作，因此每次计算的时间复杂度为O(1)。因此，总体的时间复杂度为O(n)。

      2. 空间复杂度：为了存储计算过的斐波那契数列的值，我们需要一个长度为n+1的数组。因此，空间复杂度为O(n+1)，即O(n)。

      实际运行发现当n为10000-20000耗时5毫秒，n为30000时耗时17毫秒，性能变好了，但当n为40000的时候耗时29毫秒性能上又变差了，然后n为11000万时出现OutOfMemoryError。

      这是因为在计算斐波那契数列的过程中，需要创建一个长度为n+1的数组来存储计算过的斐波那契数值，而11000万这样的大数会导致需要分配非常大的内存空间来存储数组，超出了Java虚拟机默认的堆内存大小。

      要解决这个问题，可以通过增加Java虚拟机的堆内存大小来提供更多的内存空间，可以通过设置-Xmx参数来实现。例如，可以使用命令java -Xmx4g zyfboot来将堆内存大小设置为4GB。然而，对于非常大的n值，即使增加堆内存大小也可能会遇到内存不足的问题。

      六、取消缓存直接采用迭代优化

      （一）解法思路

      取消缓存，采用迭代的方式来计算斐波那契数列是一种简单而有效的方法，通过循环迭代计算斐波那契数列的每一项，不需要额外的存储空间来缓存已经计算过的值，从而节省了内存空间，同时也提高了效率。

      • 首先，我们将斐波那契数列的前两项初始化为0和1，作为初始状态。
      • 然后，通过一个循环来迭代计算斐波那契数列的每一项。从第三项开始，每一项都是前两项的和。
      • 在计算每一项时，需要更新前两项的值，使其保持最新的状态，以便下一次迭代使用。
      • 重复以上步骤，直到计算到第n项为止。计算完成后，第n项的值即为所求的斐波那契数列的值。

        采用迭代的方式计算斐波那契数列不需要额外的存储空间，只需要少量的变量来保存前两项的值以及当前项的值。因此，它的空间复杂度为O(1)，效率很高。

        （二）代码展示

        package org.zyf.javabasic.algorithm;
import java.math.BigInteger;
/**
 * @program: zyfboot-javabasic
 * @description: 采用迭代方式计算斐波那契数列
 * @author: zhangyanfeng
 * @create: 2024-04-24 23:58
 **/
public class IterativeFibonacci {
    public static BigInteger fibonacci(int n) {
        if (n <= 1) {
            return BigInteger.valueOf(n);
        }
        BigInteger a = BigInteger.ZERO;
        BigInteger b = BigInteger.ONE;
        BigInteger temp;
        for (int i = 2; i <= n; i++) {
            temp = b;
            b = a.add(b);
            a = temp;
        }
        return b;
    }
    public static void main(String[] args) {
        int[] nValues = {10000, 20000, 80000,800000,1000000,5000000,10000000,90000000};
        for (int n : nValues) {
            long startTime = System.currentTimeMillis();
            BigInteger result = fibonacci(n);
            long endTime = System.currentTimeMillis();
            long elapsedTime = endTime - startTime;
            System.out.println("Fibonacci(" + n + ") = " );
            System.out.println("程序运行时间：" + elapsedTime + " 毫秒");
        }
    }
}

        （三）性能分析

        1. 时间复杂度：在迭代过程中，每次循环都只需要进行一次加法操作，因此每次循环的时间复杂度为O(1)。总共需要进行n-1次循环（从第3项开始到第n项），因此总体的时间复杂度为O(n)。

        2. 空间复杂度：采用迭代方式计算斐波那契数列不需要额外的存储空间来存储计算过的值，只需要少量的变量来保存前两项的值以及当前项的值。因此，空间复杂度为O(1)，即常数级别的空间复杂度。

        实际运行发现当n为10000耗5毫秒，n为20000时耗时5毫秒，当n为80000的时候耗时64毫秒，当n为80万的时候耗时4781毫秒，当n为100万的时候耗时4782毫秒，当n为500万的时候耗时182683毫秒（182.683秒），当n为1000万的时候耗时721534毫秒（721.534秒）.......。当数量级很大时，其性能也就极具恶化了。

        七、用初等代数推导公式解法

        （一）解法分析

        利用初等代数推导斐波那契数列的公式解法是一种高效的方法，可以在O(1)的时间复杂度内得到斐波那契数列的第n项的值。这种方法利用了斐波那契数列的性质和数学推导，而不需要进行递归或迭代的计算。

        斐波那契数列的公式解法基于以下两个定理：

        1. 通项公式：斐波那契数列的第n项可以通过以下通项公式来计算：

          其中，

          其为黄金分割比。

        2. 斐波那契数列的性质：当n为正整数时，。

        利用以上两个定理，可以得到斐波那契数列的公式解法：

        1. 首先，计算𝜙和−𝜙的幂次方，可以通过快速幂算法来实现。

        2. 然后，利用通项公式计算斐波那契数列的第n项的值。

        （二）代码展示

        package org.zyf.javabasic.algorithm;
import java.math.BigDecimal;
/**
 * @program: zyfboot-javabasic
 * @description: 使用初等代数推导的公式解法
 * @author: zhangyanfeng
 * @create: 2024-04-25 00:26
 **/
public class FormulaFibonacciPerformance {
    public static long getFibonacciByFormula(int index) {
        double temp = Math.sqrt(5.0);
        return (long) ((Math.pow((1 + temp) / 2, index) - Math.pow((1 - temp) / 2, index)) / temp);
    }
    public static void main(String[] args) {
        int[] nValues = {100000, 2100000000};
        for (int n : nValues) {
            long startTime = System.nanoTime();
            long result = getFibonacciByFormula(n);
            long endTime = System.nanoTime();
            long elapsedTime = endTime - startTime;
            System.out.println("Fibonacci(" + n + ") = " + result);
            System.out.println("程序运行时间：" + elapsedTime + " 纳秒");
        }
    }
}

        （三）性能分析

        1. 时间复杂度：计算黄金分割比的幂次方和斐波那契数列的第n项都可以在常数时间内完成，因此整体的时间复杂度为O(1)。

        2. 空间复杂度：该方法不需要额外的存储空间来保存斐波那契数列的中间结果，因此空间复杂度为O(1)，即常数级别的空间复杂度。

        实际运行发现当n为10万时耗时1600纳秒，n为21亿时耗时1084纳秒（0.001084 毫秒）。

        但初等代数推导的公式解法在处理较大的n值时会遇到一些问题：

        1. 黄金分割比（𝜙）是一个无理数，其幂次方的计算会导致精度丢失问题。计算机的浮点数表示有限，超过一定的位数后会出现精度丢失，导致计算结果不准确。

        2. 由于精度丢失和计算效率问题，当n超过一定大小（如n>71）时，计算结果会变得不可靠，与真实的斐波那契数列的值存在较大偏差。

        3. 尽管空间复杂度为O(1)，但计算黄金分割比的幂次方和斐波那契数列的第n项所涉及的数值非常大，可能需要大量的内存空间来存储这些数值，导致内存消耗增加。

        虽然初等代数推导的公式解法具有常数级别的时间复杂度和空间复杂度，但在处理较大的n值时会遇到精度丢失、计算效率低下、结果不可靠等问题，因此不适用于处理超过一定大小的n值。

        八、矩阵解法

        （一）解法分析

        利用矩阵的特性和矩阵乘法的性质，将斐波那契数列的计算问题转化为矩阵乘法的问题，从而避免了传统递归或迭代算法中的重复计算，提高了计算效率。该方法的基本思想是将斐波那契数列的递推关系表示为矩阵形式，然后通过矩阵的幂运算来快速计算出第n项的值。

        具体而言，矩阵解法首先定义一个2x2的矩阵F，称为斐波那契矩阵，其元素为

        然后，利用矩阵的幂运算，通过快速幂算法来计算斐波那契数列的值。在计算过程中，需要注意选择合适的数据类型以避免数值溢出的问题。

        实现步骤：

        • 首先，对输入的n值进行有效性检查，确保其为正整数。
        • 初始化斐波那契矩阵如上图，记为initMatrix。
        • 迭代计算矩阵initMatrix的n-2次幂（因为斐波那契数列从第3项开始才适用矩阵解法），得到结果矩阵tem。
        • 最终结果存储在tem矩阵的第一行第一列位置，即tem[0][0]，返回该值作为第n项的斐波那契数。

          （二）代码展示

          package org.zyf.javabasic.algorithm;
/**
 * @program: zyfboot-javabasic
 * @description: 使用矩阵解法计算斐波那契数列
 * @author: zhangyanfeng
 * @create: 2024-04-25 00:54
 **/
public class MatrixFibonacci {
    public static long getFibonacciByMatrix(int index) {
        // 检查输入的索引是否合法
        if (index <= 0) {
            throw new IllegalArgumentException("Index must be a positive integer");
        }
        // 初始斐波那契矩阵
        long[][] fibonacciMatrix = {{1, 1}, {1, 0}};
        // 迭代计算矩阵的 index - 2 次幂
        for (int i = 2; i < index; i++) {
            fibonacciMatrix = matrixMultiply(fibonacciMatrix, new long[][]{{1, 1}, {1, 0}});
        }
        // 结果存储在矩阵的第一行第一列位置
        return fibonacciMatrix[0][0];
    }
    // 矩阵乘法
    private static long[][] matrixMultiply(long[][] a, long[][] b) {
        long[][] result = new long[2][2];
        result[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
        result[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
        result[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
        result[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
        return result;
    }
    public static void main(String[] args) {
        // 计算第100000项的斐波那契数
        long startTime1 = System.currentTimeMillis();
        long fibonacci100000 = MatrixFibonacci.getFibonacciByMatrix(100000);
        long endTime1 = System.currentTimeMillis();
        long elapsedTime1 = endTime1 - startTime1;
        System.out.println("Fibonacci(100000) = " + fibonacci100000);
        System.out.println("耗时：" + elapsedTime1 + "毫秒");
        // 计算第2100000000项的斐波那契数
        long startTime2 = System.currentTimeMillis();
        long fibonacci2100000000 = MatrixFibonacci.getFibonacciByMatrix(2100000000);
        long endTime2 = System.currentTimeMillis();
        long elapsedTime2 = endTime2 - startTime2;
        System.out.println("Fibonacci(2100000000) = " + fibonacci2100000000);
        System.out.println("耗时：" + elapsedTime2 + "毫秒");
    }
}

          （三）性能分析

          1. 时间复杂度：因为矩阵解法使用快速幂算法来计算斐波那契数列的第n项，每次迭代都会将指数除以2，因此迭代次数为log₂n。

          2. 空间复杂度：矩阵解法不需要保存额外的中间结果，只需要使用一个固定大小的矩阵来进行计算，因此空间复杂度是常数级别的。

          实际运行发现当n为10万时耗时19毫秒，n为21亿时耗时14947毫秒。

          矩阵解法的优点在于其时间复杂度为O(log n)，相较于传统的递归或迭代算法更为高效。此外，由于不需要保存中间结果，节省了内存空间。然而，需要注意的是，在计算过程中可能会出现数据溢出或精度问题，特别是对于非常大的n值。因此，在实际应用中，需要谨慎选择数据类型和算法，并根据具体情况进行优化。

          九、矩阵解法+快速幂

          （一）解法分析

          基本思想是利用矩阵乘法的性质，将斐波那契数列的递推关系表示为矩阵形式，然后通过快速幂算法来快速计算矩阵的高次幂，从而得到斐波那契数列的第n项的值。

          具体而言，该方法首先定义一个2x2的斐波那契矩阵F，其元素为

          然后利用快速幂算法来计算矩阵F的高次幂，即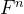F^{n}。通过将指数n转化为二进制形式，并利用矩阵的乘法性质，可以在O(log n)的时间复杂度内计算出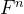F^{n}。最后，将得到的矩阵𝐹𝑛Fn与初始矩阵(10)(10​)相乘，得到的结果的第一个元素即为斐波那契数列的第n项的值。

          在实际应用中，结合快速幂的矩阵解法是计算斐波那契数列的最优解之一，特别是对于大数值的情况。

          （二）代码展示

          package org.zyf.javabasic.algorithm;
/**
 * @program: zyfboot-javabasic
 * @description: 使用矩阵解法结合快速幂
 * @author: zhangyanfeng
 * @create: 2024-04-25 01:06
 **/
public class MatrixFibonacciWithFastPower {
    private static final long[][] INIT_MATRIX = {{1, 1}, {1, 0}};
    private static final long[][] UNIT_MATRIX = {{1, 0}, {0, 1}};
    public static long getFibonacciByMatrixAndFastPower(int index) {
        // 检查索引的有效性
        if (index <= 0) {
            throw new IllegalArgumentException("Index must be a positive integer");
        }
        // 边界情况处理
        if (index == 1 || index == 2) {
            return 1;
        }
        // 初始结果为单位矩阵
        long[][] result = UNIT_MATRIX;
        long[][] temp = INIT_MATRIX;
        int m = index - 2;
        // 利用快速幂算法计算矩阵的高次幂
        while (m != 0) {
            if ((m & 1) == 1) {
                result = matrixMultiply(temp, result);
            }
            temp = matrixMultiply(temp, temp);
            m >>= 1;
        }
        // 结果矩阵的第一个元素即为斐波那契数列的第n项的值
        return result[0][0];
    }
    // 矩阵乘法
    private static long[][] matrixMultiply(long[][] a, long[][] b) {
        long[][] result = new long[2][2];
        result[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
        result[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
        result[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
        result[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
        return result;
    }
    public static void main(String[] args) {
        // 计算第100000项的斐波那契数
        long startTime1 = System.nanoTime();
        long fibonacci100000 = MatrixFibonacciWithFastPower.getFibonacciByMatrixAndFastPower(100000);
        long endTime1 = System.nanoTime();
        double elapsedTime1 = (endTime1 - startTime1) / 1_000_000.0; // 转换为毫秒
        System.out.println("Fibonacci(100000) = " + fibonacci100000);
        System.out.println("耗时：" + elapsedTime1 + "毫秒");
        // 计算第2100000000项的斐波那契数
        long startTime2 = System.nanoTime();
        long fibonacci2100000000 = MatrixFibonacciWithFastPower.getFibonacciByMatrixAndFastPower(2100000000);
        long endTime2 = System.nanoTime();
        double elapsedTime2 = (endTime2 - startTime2) / 1_000_000.0; // 转换为毫秒
        System.out.println("Fibonacci(2100000000) = " + fibonacci2100000000);
        System.out.println("耗时：" + elapsedTime2 + "毫秒");
    }
}

          （三）性能分析

          1. 时间复杂度分析：计算第n项斐波那契数需要进行快速幂运算，时间复杂度为O(log n)。这是因为快速幂算法的时间复杂度为O(log n)，在算法中只需进行log n次乘法运算。在快速幂运算中，每次矩阵相乘的时间复杂度为O(1)。因此，总的时间复杂度为O(log n)。
          2. 空间复杂度分析：算法中使用的空间主要由两个矩阵所占用的空间决定。这两个矩阵分别是初始矩阵和结果矩阵，都是固定大小的2x2矩阵。因此，空间复杂度为O(1)，即常数级别的空间复杂度。

          实际运行发现当n为10万时耗时0.013125毫秒，n为21亿时耗时0.022042毫秒。

          矩阵解法结合快速幂的斐波那契数列算法具有优秀的时间复杂度O(log n)和空间复杂度O(1)，适用于需要高效计算大数值斐波那契数列的场景。

          十、最优解分析

          在实际应用中，结合快速幂的矩阵解法确实是计算斐波那契数列的最优解之一，尤其是对于大数值的情况。然而，并不是所有情况下都适合使用这种方法。

          • 对于小规模的斐波那契数列计算（比如前几十项），简单的递归或迭代方法可能更为简单和高效。
          • 对于需要计算大数值斐波那契数列的情况，结合快速幂的矩阵解法通常是最优的选择之一，因为它具有较低的时间复杂度和空间复杂度。

            然而，在某些特定情况下，可能存在其他更为优化的解法。例如，针对特定斐波那契数列的性质和规律，可能会有更快速的算法或更有效的数学公式可以利用。因此，虽然矩阵解法结合快速幂是一种非常有效的方法，但并不排除其他可能存在的最优解法。

相关推荐

关于我们常见问题广告服务免责声明联系我们
Powered By Z-BlogPHP 1.7.3 Theme By 优美主题
Copyright Your WebSite.Some Rights Reserved. 浙ICP备2023018783号